probability - Proof explanation - weak law of large numbers

Let $(X_i)$ be i.i.d. random variables with mean $\mu$ and finite variance. Then $$\dfrac{X_1 + \dots + X_n}{n} \to \mu \text{ weakly }$$ I have the proof here: What I don't understand is, why it

i.ytimg.com/vi/ihTpK6dXSas/hq720.jpg?sqp=-oaymwEhC

Proof of Strong law of large numbers and weak law of large numbers

Stats Syllabus, PDF, Probability Theory

Proof of the Law of Large Numbers Part 1: The Weak Law, by Andrew Rothman

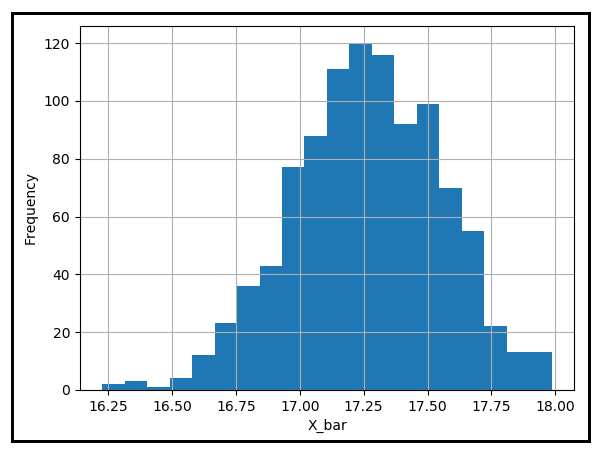
Unraveling the Law of Large Numbers, by Sachin Date

2.6. Probability and Statistics — Dive into Deep Learning 1.0.3 documentation

Weak Law of Large Numbers (WLLN). Overview, by Pablo Kowalski Kutz

real analysis - Proof of the strong law of large numbers for bernoulli random variables - Mathematics Stack Exchange

/images/equations/WeakLawofLa

Proof of the Law of Large Numbers Part 2: The Strong Law, by Andrew Rothman