The compression factor (compressibility factor) for 1 mol of a van der

For 1 mol of a gas, the van der Waals equation is (P+(a)/(V(m)^(2)))(V(m)-b)=RT Ignoring b, we get (given volume of gas molecule is negligible) (P+(a)/(V(m)^(2)))V(m)=RT ltbgt or pV(m)+(a)/(V(m))=RT or (pV(m))/(RT)+(a)/(V(m)RT)=1 or Z=(pV(m))/(RT)=1-(a)/(V(m)RT) (i) It is given that Z=(pV(m))/(RT)=0.5implies V(m)=(0.5RT)/(P) With this, equation (i) becomes 0.5=1-(a)/((0.5RT//p)RT) or a=(0.5)((0.5RT)/(p))RT=0.25(R^(2)T^(2))/(p) Substiuting the given values, we get a=(0.25)[((0.082L atm K^(-1)mol^(-1))^(2)(273 K)^(2))/((100 atm))] =1.2528 L^(2) atm mol^(-2)

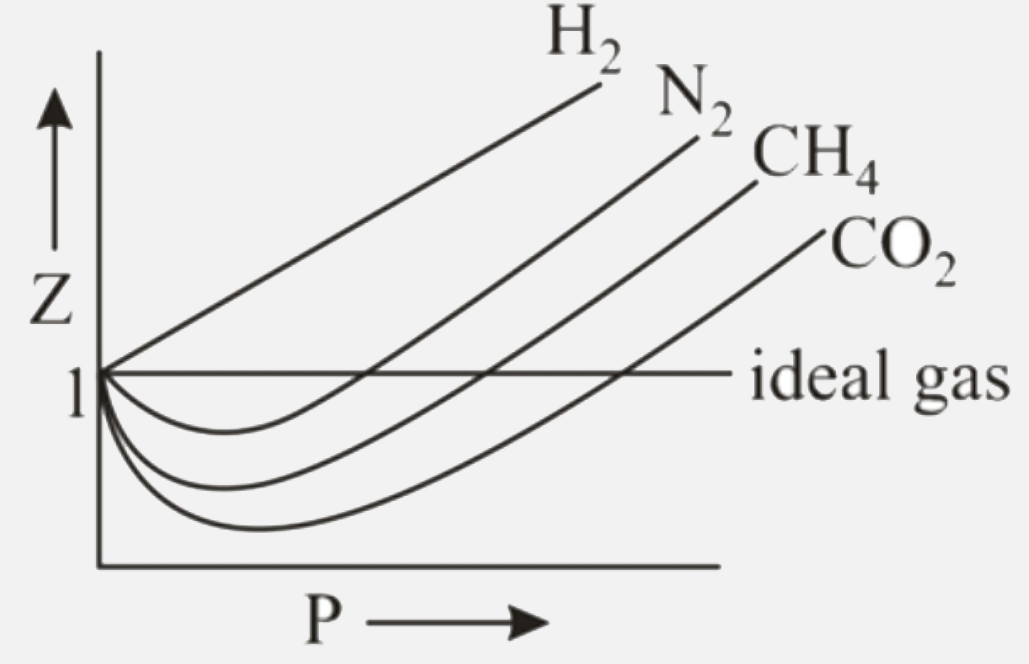
For the gas C, which is typical real gas for which neither a nor b=0.

One mole of a monoatomic real gas satisfies the equation p(V-b)=RT wh

A 2.0 L container at 25^(@)C contain 1.25 mol of O(2) and 3.2 mol of C

Malayalam] The compressibility factor for definite amount of van der

For one mole of a van der Waals gas when b =0 and T =30 K the PV vs1//

The van der Waals equation for one mol of CO(2) gas at low pressure wi

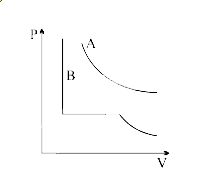
For two gases A and B,P v//s V isotherms are drawn at T K as shown, T

The root mean square velocity of the molecule is inversely proportiona

is characterised by van der Waals coefficients that are dependent on t

The compression factor (compressibility factor) for 1 mol of a van der

Longest mean free path stands for

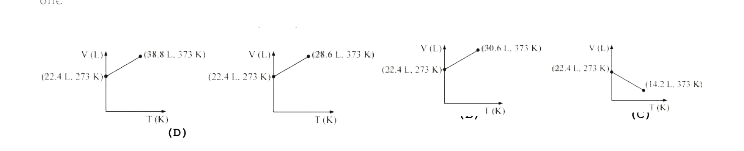
The compressibility factor of gases is less than unity at STP. Therefo

The compressibility factor for definite amount of van der Waals' gas a